Régularisation d’un modèle
Contents
Régularisation d’un modèle¶
La régularisation est une des méthodes les plus utilisées pour réduire le sur-apprentissage d’un modèle. Dans ce chapitre, nous allons explorer les régularisations classiques et observer leur impact sur les performances d’un modèle.
Comment fonctionne la régularisation¶
Le principe général est de contraindre les paramètres appris par un modèle. Pour ce faire, on peut ajouter un terme supplémentaire dans la fonction de loss que l’on souhaite minimiser. Ce terme supplémentaire compte comme une pénalité, elle permet de réduire l’overfitting.
Mais pourquoi ajouter une pénalité permet de réduire l’overfitting ?
Cela peut paraître contre-intuitif, mais en fait réduire les capacités d’apprentissage d’un modèle peut l’aider à mieux généraliser ! Si on reprend notre exemple du chapitre sur la généralisation, on peut imaginer qu’ajouter une pénalité à notre modèle revient à l’obliger à travailler avec un kit réduit d’outils à sa disposition. Il va être obliger de faire avec moins, et donc il ne pourra pas sur-optimiser son apprentissage sur les exercices d’entraînement (les petites corrélations qui améliorent marginalement les performances mais qui se trouvent inutiles voire désastreuses lors de l’évaluation sur de nouveaux exercices).
D’une certaine manière, ajouter une pénalité sur les paramètres du modèle revient à demander au modèle de trouver une solution simple et efficace au problème donné. Cette solution est généralement la meilleure !
Nous allons voir particulièrement deux façons de régulariser un modèle : la régularisation L1 et L2. Nous les verrons appliquées à la regression linéaire, mais il faut savoir que ces méthodes sont générales et s’appliquent à tout type de modèle paramétrique.
Dataset exemple¶
Afin de mieux se rendre compte de l’impact de la régularisation sur nos modèles, nous utilisons un dataset fictif. Pour simplifier la lecture, nous n’utilisons pas de jeu de validation ici, car nous choisissons d’uniquement comparer les performances finales de généralisation de nos modèles sans faire de recherche d’hyperparamètre. Cependant, gardez en tête qu’en cas réel, il faut aussi générer le jeu de validation et n’évaluer qu’un modèle final sur le jeu de test.
Le dataset est généré en ajoutant un fort bruit pour empêcher nos modèles linéaires de pouvoir prédire parfaitement y.
Cela permet de faciliter l’overfitting de nos modèles si nous ne sommes pas prudent.
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
X, y = make_regression(
n_samples=15,
n_features=10,
n_informative=7,
noise=15,
random_state=1
)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=1)
Régularisation L2¶
La régularisation L2 demande à ce que la somme des carrés des paramètres soit la plus petite possible. C’est une fonction quadratique, elle est donc continue et dérivable en tout point ce qui est souvent apprécié.
Mathématiquement on peut écrire :
Afin de moduler la force de pénalisation par rapport à la loss initiale, on définit un hyperparamètre \(\lambda\) qui est une constante positive choisie avant l’entraînement. Un \(\lambda\) trop gros empêchera le modèle d’apprendre (il ne pourra plus s’exprimer car la moindre modification de ses poids sera fortement pénalisée), mais un \(\lambda\) trop faible masquera l’effet de la régularisation.
Cette régularisation (ainsi que la L1 juste après) pousse le modèle à apprendre des coefficients pas trop éloignés de 0. Il doit équilibrer son entraînement afin de réduire la loss principale et éviter d’avoir une pénalité élevée. Intuitivement, le modèle est contraint à simplifier sa prédiction. Il ne peut pas affiner ses prédictions, ce qui le rend moins précis sur le jeu d’entraînement mais qui réduit la chance de sur-apprentissage.
On parle de Ridge Regression lorsque l’on fait une régression linéaire couplée à une régularisation L2.
Exemple¶
Dans scikit-learn, le modèle permettant de faire une régression linéaire avec régularisation L2 se nomme Ridge.
from sklearn.linear_model import Ridge
def train_ridge(lambda_value: float):
print(f'Ridge regression avec une valeur de lambda = {lambda_value}')
model = Ridge(lambda_value)
model.fit(X_train, y_train)
coefs = model.coef_
print(f'L2(w) = {(coefs ** 2).sum():.2f}')
r2 = model.score(X_train, y_train)
print(f"R² sur le jeu d'entraînement: {r2:.3f}")
r2 = model.score(X_test, y_test)
print(f"R² sur le jeu de test: {r2:.3f}")
train_ridge(0)
print('')
train_ridge(1)
Ridge regression avec une valeur de lambda = 0
L2(w) = 49709.83
R² sur le jeu d'entraînement: 1.000
R² sur le jeu de test: 0.476
Ridge regression avec une valeur de lambda = 1
L2(w) = 15137.40
R² sur le jeu d'entraînement: 0.972
R² sur le jeu de test: 0.786
Le modèle sans régularisation (\(\lambda = 0\)) a sur-appris par rapport au second modèle ! On s’aperçoit que c’est bien le modèle ayant la pénalité \(\text{L2}(w)\) la plus faible qui généralise mieux.
Régularisation L1¶
La régularisation L1 contraint la norme L1 des paramètres à être la plus petite possible. Elle n’est pas dérivable en 0, mais ce n’est pas gênant en pratique.
Cette régularisation a tendance à pousser des coefficients \(w\) à valoir 0 exactement, ce qui est utile pour faire de la sélection de features. En effet, si une feature a un coefficient associé qui vaut exactement 0, alors on peut se débarasser de cette feature car elle n’influe clairement pas le calcul des prédictions !
On parle de Lasso Regression lorsque l’on fait une régression linéaire couplée à une régularisation L1.
Exemple¶
from sklearn.linear_model import Lasso, LinearRegression
def train_lasso(lambda_value: float):
print(f'LASSO regression avec une valeur de lambda = {lambda_value}')
if lambda_value == 0: # Problème de convergence du LASSO lorsque lambda = 0
model = LinearRegression()
else:
model = Lasso(lambda_value)
model.fit(X_train, y_train)
coefs = model.coef_
print(f'L2(w) = {(coefs ** 2).sum():.2f}')
print(f'Coefs nuls: {(coefs == 0).sum()}')
r2 = model.score(X_train, y_train)
print(f"R² sur le jeu d'entraînement: {r2:.3f}")
r2 = model.score(X_test, y_test)
print(f"R² sur le jeu de test: {r2:.3f}")
train_lasso(0)
print('')
train_lasso(3)
LASSO regression avec une valeur de lambda = 0
L2(w) = 49709.83
Coefs nuls: 0
R² sur le jeu d'entraînement: 1.000
R² sur le jeu de test: 0.476
LASSO regression avec une valeur de lambda = 3
L2(w) = 18262.30
Coefs nuls: 2
R² sur le jeu d'entraînement: 0.981
R² sur le jeu de test: 0.816
Comme pour l’exemple précédent, le modèle qui généralise le mieux est celui qui est régularisé. On remarque de plus que le modèle régularisé a décidé que deux des features étaient inintéressantes pour la prédiction. C’est cohérent car nous avons généré le dataset à l’aide de 7 features informatives parmis 10 features au total (il y a donc 3 features qui ne servent pas à la prédiction, et qui sont présentes uniquement pour brouiller le modèle).
L1 vs L2 : que choisir ?¶
Nous connaissons maitenant deux méthodes qui permettent de régulariser facilement un modèle.
Comment choisir entre les deux ? Laquelle est la meilleure ?
Pour mieux comprendre la différence entre les deux méthodes on peut visualiser les solutions engendrées par l’utilisation de l’une ou l’autre façon de régulariser.
Visualisation L1 vs L2¶
Pour mieux visualiser leur effet sur l’entraînement de nos modèles, nous pouvons considérer un cas simple où nous avons deux paramètres \(w_1\) et \(w_2\) à entraîner. On peut reformuler les problèmes de minimisation comme des problèmes de minimisation sous contraintes :
Ces deux façons de voir le problème sont équivalentes. \(\beta\) est inversement proportionnel à \(\lambda\). On peut ainsi tracer les courbes de niveaux du loss en fonction des valeurs de \(w_1\) et \(w_2\) et visualiser les zones où les contraintes sont satisfaites (l’espace des solutions réalisables).
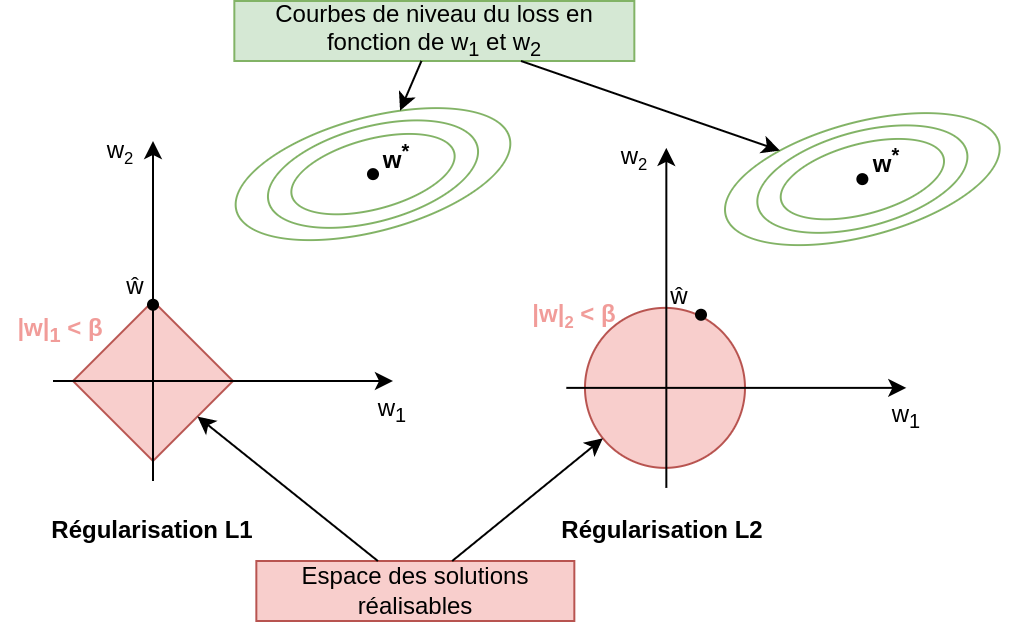
Fig. 4 Visualisation de la régularisation L1 (à gauche) et L2 (à droite).¶
Comme on peut le voir, la régularisation L1 impose des solutions dans un espace en forme de diamant, alors que la L2 génère un espace de solutions en forme de cercle. La solution optimale sans régularisation est représentée par le point \(w^*\). Le loss ici est une simple MSE, dont les courbes de niveaux tracent des ellipses de plus en plus grandes autour du minimum \(w^*\). La solution obtenue avec régularisation est représentée par le point \(\hat w\).
Visuellement, la solution optimale \(\hat w\) est à la jonction entre les courbes de niveau du loss et la frontière de l’espace des solutions.
Ainsi, il est aisé de comprendre pourquoi la régularisation L1 pousse plus facilement les coefficients \(\hat w\) vers 0. En prenant un point \(w^*\) au hasard sur le plan 2D, il est plus probable que la projection des courbes de niveaux sur le diamant arrive sur un des angles !
Comment choisir ?¶
En pratique, les deux méthodes peuvent donner de meilleurs résultats. Dans notre exemple, c’est la normalisation L1 qui s’en sort le mieux (puisque son \(R^2\) est plus élevé sur le jeu de test), mais ça pourrait très bien être l’inverse ! Le mieux est de tester les deux méthodes et de comparer les performances des modèles sur le jeu de validation.
Rien n’empêche d’utiliser à la fois la régularisation L1 et L2. Lorsque les deux méthodes sont utilisées pour une régression linéaire, on dit que l’on utilise une méthode Elastic Net. En pratique, c’est Elastic Net qui a tendance à donner de meilleurs résultats que la L1 ou la L2 pris séparéments.
Les deux méthodes ont quand même chacune leur avantage :
L2 est dérivable en tout point, ce qui peut aider pour certains algorithmes d’optimisation.
L1 permet de sélectionner les features utiles pour la prédiction.
Parce que la L2 est dérivable partout, elle est généralement préférée. Elle permet de ne pas se soucier du cas particulier où la dérivée n’est pas définie. Cependant, sachez en pratique ne pas être dérivable en un unique point est rarement dérangeant.
Et les autres régularisations ?¶
Il est possible de régulariser le modèle de plusieurs façons possibles. Les autres façons de régulariser dépendent beaucoup du modèle et de la tâche qui sont considérés.
Par exemple dans le chapitre sur la généralisation, nous avons régularisé nos régressions polynomiales sans même le savoir. En effet, on a contraint les capacités du modèle en choisissant de limiter le degré maximal de notre polynôme ! (Peut-on vraiment parler de régularisation pour ce cas là ?)
D’autres régularisations existent donc. Elles sont souvent spécifiques au type de modèle choisi, et se découvrent donc petit à petit en même temps que l’on apprend à utiliser d’autres modèles. La L1 et L2 sont quand même les deux régularisations les plus utilisées et il est important de les connaître.
Conclusion¶
La régularisation est une technique permettant de réduire l’overfitting des modèles de ML.
En général, le but d’une régularisation est de réduire la complexité du modèle. Elle s’exprime sous forme de pénalité ajoutée à la loss du modèle.
Les deux méthodes de régularisation les plus utilisées sont la L1 et L2. Elles poussent toutes les deux les coefficients des modèles vers 0.
