Compromis biais-variance
Contents
Compromis biais-variance¶
Le compromis biais-variance est un résultat fondamental en Machine Learning. Il décompose les erreurs d’un modèle en trois catégories : le biais inductif, la variance et le bruit.
Les biais inductifs d’un modèle caractérisent l’espace des fonctions apprenables par un modèle.
La variance est une mesure de la sensibilité que possède un modèle par rapport aux données utilisées pour l’entraîner.
Biais inductif¶
Il est en fait impossible d’entraîner un modèle sans biais inductif. Sans cela, il existerait une infinité de fonctions qui seraient capables de modéliser les relations entres des couples \((x, y)\) quelconques. L’ensemble des biais inductifs forment une contrainte sur les caractéristiques que doivent avoir un modèle. L’étape d’apprentissage se résume alors à la recherche de la meilleure fonction parmis l’espace des fonctions modélisables.
Espace de recherche de fonction¶
Il est important d’avoir une intuition de ce que l’on entends par espace de recherche de fonction.
On peut décrire le processus d’apprentissage d’un modèle comme une façon de trouver la meilleure fonction qui modélise la relation souhaitée entre nos couples \((x, y)\). Il y a donc au départ de l’apprentissage tout un ensemble de fonctions modélisables par notre modèle. Cet ensemble peut être vu comme un espace de recherche.
Par exemple, dans le cas de la régression linéaire, la fonction est décrite par les coefficients de la droite modélisée. Dans ce cas, l’espace des fonctions modélisables est décrit par toutes les fonctions linéaires définies par les valeurs que peuvent prendre les coefficients. Durant l’apprentissage d’une régression linéaire, le modèle va trouver les meilleures valeurs des coefficients afin de minimiser le loss d’entraînement, et donc finir par choisir une fonction dans cet espace.
Caractérisation de l’espace de recherche¶
Les biais expriment des contraintes sur les fonctions que peuvent modéliser nos algorithmes. Un modèle linéaire fait l’hypothèse que la relation \((x, y)\) peut être facilement décrite à l’aide d’une droite. Ainsi, l’espace de recherche ne contient que des fonctions affines.
L’espace de recherche définit l’expressivité d’un modèle. Le plus cet espace est divers et complexe, le mieux notre modèle sera capable d’apprendre des relations complexes entre nos couples \((x, y)\). Pour avoir un tel espace de recherche, il faut n’imposer que des biais peut contraignants. On a alors un modèle très maléable. Cependant, on se rend vite compte que si notre modèle est trop maléable, il risquera de facilement sur-apprendre car il aura trop finement adapter son modèle aux données d’entraînement.
Les biais inductifs nous permettent donc choisir la forme de l’espace de fonctions modélisables. Ajuster nos biais permet de contrôler le sur-apprentissage ainsi que le sous-apprentissage.
Biais courants¶
Le biais le plus courant est celui de la continuité : on suppose que si deux points \(x\) et \(x'\) sont proches dans l’espace, alors il est probable que \(f(x)\) et \(f(x')\) soient proches l’un de l’autre. Intuitivement, cela revient à dire que si deux images ne diffèrent que de quelques pixels, alors si l’une des deux images représente un chien, la seconde sera très probablement une image de chien.
Un autre biais omniprésent est celui de la régularisation. La régularisation est en fait une façon de biaiser notre modèle vers des solutions plus simples. C’est aussi une hypothèse que l’on choisit lorsque l’on entraîne le modèle !
Variance¶
La variance d’un modèle résume son besoin de données pour apprendre au mieux. Plus un modèle a de variance et plus il aura besoin de grosses quantités de données afin de ne pas sur-apprendre.
Pour être plus précis, on considère que les données utilisées à l’apprentissage proviennent toutes d’une source aléatoire capable de générer toutes les données possibles d’une distribution fixée. On peut alors échantillonner plusieurs jeux de données à partir de cette source. Cela permet alors d’entraîner autant de modèles qu’il y a de jeux de données. Chaque modèle va converger vers une fonction finale qui peut être évalué sur un ensemble de test commun. Dans ce cas, la variance d’un modèle de ML est mesurée par la variance des performances des différents modèles évalués sur le jeu de test, mais entraînés sur des données différentes.
Si les prédictions d’un modèle sont trop dépendantes des données utilisées pour l’entraîner, alors c’est qu’il est en sur-apprentissage, car cela signifie qu’il s’est trop spécialisé sur les données fournies d’entraînement.
Exemple: régression linéaire vs KNN¶
On va illustrer l’impact des biais et de la variance dans un exemple en utilisant un jeu de données non linéaire.
from sklearn.datasets import make_friedman1
from sklearn.model_selection import train_test_split
def make_dataset(n_samples: int) -> tuple:
X, y = make_friedman1(
n_samples=n_samples,
n_features=10,
random_state=42,
)
return train_test_split(X, y, test_size=0.2)
def plot_perf(model, X_train, y_train, X_test, y_test):
model.fit(X_train, y_train)
r2 = model.score(X_train, y_train)
print(f'Entraînement : {r2:.3f}')
r2 = model.score(X_test, y_test)
print(f'Test: {r2:.3f}')
n_samples_small = 50
n_samples_big = 10000
Régression linéaire¶
Le modèle utilisé lors de la régression linéaire ne peut apprendre que des fonctions de la forme \(f(x) = ax + b\) (ici nous n’avons qu’une feature \(x\)). Pour ce modèle, le biais inductif est l’hypothèse que les données peuvent se modéliser sous la forme d’une droite. L’espace de recherche est donc extrêmement contraint ! Mais l’avantage d’un tel modèle c’est qu’il suffit de peu de points pour rapidement converger vers une fonction \(f\) de bonne qualité. En effet, il suffit de deux points pour tracer une droite ! Dans la vie réelle, les points sont bruités donc il faut plus de points pour mieux estimer la droite, mais l’idée reste la même.
from sklearn.linear_model import LinearRegression
print('Modèle linéaire')
model = LinearRegression()
print(f'\nPetit jeu de données ({n_samples_small} exemples)')
X_train, X_test, y_train, y_test = make_dataset(n_samples_small)
plot_perf(model, X_train, y_train, X_test, y_test)
print(f'\nGros jeu de données ({n_samples_big} exemples)')
X_train, X_test, y_train, y_test = make_dataset(n_samples_big)
plot_perf(model, X_train, y_train, X_test, y_test)
Modèle linéaire
Petit jeu de données (50 exemples)
Entraînement : 0.789
Test: 0.750
Gros jeu de données (10000 exemples)
Entraînement : 0.751
Test: 0.761
K-NN¶
On peut comparer cet exemple à celui du KNN. Le KNN ne fait que l’hypothèse de continuité, il prédit la valeur d’un point \(x\) par rapport aux autres points vus pendant l’entraînement qui sont au voisinage de \(x\). C’est l’hypothèse la plus simple qui soit, et elle laisse place à un ensemble de fonctions modélisables énorme. Cela permet de garder un fort potentiel de modélisation, mais ça demande aussi un nombre de données très élevé pour modéliser précisément une fonction en tout point. En fait, à cause de la malédiction de la dimension, le nombre de données nécessaires pour couvrir l’ensemble de définition d’un KNN croît exponentiellement avec le nombre de dimensions de nos features.
from sklearn.neighbors import KNeighborsRegressor
print('K-Nearest Neighbor')
model = KNeighborsRegressor(5)
print(f'\nPetit jeu de données ({n_samples_small} exemples)')
X_train, X_test, y_train, y_test = make_dataset(n_samples_small)
plot_perf(model, X_train, y_train, X_test, y_test)
print(f'\nGros jeu de données ({n_samples_big} exemples)')
X_train, X_test, y_train, y_test = make_dataset(n_samples_big)
plot_perf(model, X_train, y_train, X_test, y_test)
K-Nearest Neighbor
Petit jeu de données (50 exemples)
Entraînement : 0.472
Test: 0.437
Gros jeu de données (10000 exemples)
Entraînement : 0.893
Test: 0.846
À travers ces deux exemples, on peut voir qu’il peut y avoir des comportements drastiquement différents lors de l’entraînement de nos modèles. Avec peu de points et une hypothèse forte sur la relation entre nos données, on peut utiliser un modèle simple qui va converger sans problème. Cependant, si nous faisons une hypothèse trop forte ou mauvaise, on peut se retrouver avec un modèle trop contraint qui ne pourra pas trouver de bonne façon de modéliser le problème. Il faudra alors trouver (ou tester) de meilleures hypothèses, ou adoucir celles déjà faites. Le cas le plus simple est alors d’entraîner un modèle plus expressif comme le KNN, mais il faut alors assez de données pour que ce dernier soit capable d’apprendre une relation utile sans sur-apprendre.
Notre dataset d’exemple n’étant pas linéaire, le biais du modèle linéaire est trop contraignant dans un régime où nous avons suffisamment de données pour modéliser des modèles plus complexes.
Tradeoff biais-variance¶
Le compromis biais-variance est fondamental en Machine Learning.
Intuitivement, on a un équilibre à trouver dans la taille de l’espace des fonctions que peuvent modéliser nos modèles. Si on laisse cet espace être trop grand, alors le modèle va trouver une fonction qui sera très performante sur les données d’entraînement mais qui aura un loss élevé sur de nouvelles données à cause d’un sur-apprentissage sévère. A l’inverse, à trop réduire cet espace, on ne va laisser au modèle que des fonctions sous-efficaces pour modéliser la relation entre nos couples \((x, y)\).
Idéalement, on voudrait appliquer uniquement des biais qui correspondent à la nature de la vraie relation entre nos données. Cependant il faut garder en tête que ces biais sont souvent inconnus, nous ne pouvons donc que tester différentes hypothèses afin de regarder ce qui fonctionne le mieux en pratique sur les données à considérer.
Une relation linéaire est peut-être sous-efficace par rapport à la vraie relation de votre couple \((x, y)\), mais elle est peut-être ce que vous aurez de mieux entre le compromis “biais simplificateur” vs “nombre de données”.
Décomposition de l’erreur d’un modèle¶
Le compromis biais-variance est le résultat d’une décomposition de l’erreur d’un modèle \(h\) :
Les mauvaises performances du modèle évalué sur le jeu de test s’expliquent par la variance du modèle, son biais et le bruit intrinsèque des données. Comme nous l’avons expliqué jusqu’à présent, plus notre modèle a de biais ou de variance et plus il fera d’erreurs sur le jeu de test.
Pour réduire l’erreur liée à la variance, il faudrait pouvoir entraîner le modèle sur l’ensemble des données imaginables pour la tâche en question.
Pour réduire l’erreur liée au biais, il faudrait connaître parfaitement les caractéristiques de la relation de nos couples \((x, y)\).
Il est impossible de réduire l’erreur liée au bruit ! Ce bruit décrit la part d’inexplicabilité dans la relation entre \(x\) et \(y\).
Ce que définit cette équation, c’est simplement qu’il est possible de réduire les pertes d’un modèle en réduisant sa variance et son biais. Ce n’est pas une preuve qu’il y a forcément un compromis à faire entre la variance et les biais. Ce compromis est intrinsèque à la définition de ces termes : l’un réduit l’espace de recherche et l’autre l’augmente.
Et le bruit alors ?
Il est fort probable les features \(x\) ne permettent pas de pleinement expliquer la quantité \(y\). Dans ce cas, on aura beau essayer de réduire l’erreur au maximum, on aura toujours une petite erreur liée au bruit. Le bruit peut provenir de deux sources différentes :
Un manque de features pour décrire au mieux la situation qui a mené à \(y\). Par exemple, une photo n’est qu’une coupe 2D d’un environnement 3D (voire 4D si l’on inclus le temps). Cette coupe peut être insuffisante pour décrire au mieux ce que l’on souhaite (comment deviner ce que fait une personne qui nous tourne le dos ?).
Un bruit purement stochastique dans la source qui a générée \(y\). On peut voir ça comme l’imprécision de la mesure de \(y\), ou alors simplement un phénomène aléatoire qui se produit lors de la production de \(y\).
Ce bruit peut être vu ainsi : lorsque j’observe les mêmes \(x\), je vais tout de même obtenir des \(y\) différents. Le meilleur modèle possible ne peut alors que prédire la valeur moyenne de \(y\) sachant \(x\).
Mais alors on ne peut pas avoir de modèle parfait ?
Et non ! Un adage très connu en statistique décrit la situation ainsi : Tous les modèles sont faux, mais certains sont utiles.
Il est impossible en pratique de parfaitement modéliser la relation \((x, y)\). Et on ne parle pas que du bruit irréductible, mais même de la fonction réelle qui décrit au mieux la relation entre \(x\) et la valeur moyenne \(\hat y\) sachant \(x\). Il faudrait avoir toutes les données possibles (pouvez-vous me trouver toutes les photos de chats et de chiens possibles ?), ou faire les bonnes hypothèses sur la relation afin d’injecter les bons biais au modèle.
Enfin, il est intéressant de voir qu’une partie du sur-apprentissage est en fait dû au modèle qui s’affine sur le bruit. Il aura alors réduit les erreurs liées au bruit du jeu d’entraînement, mais il aura appris n’importe quoi !
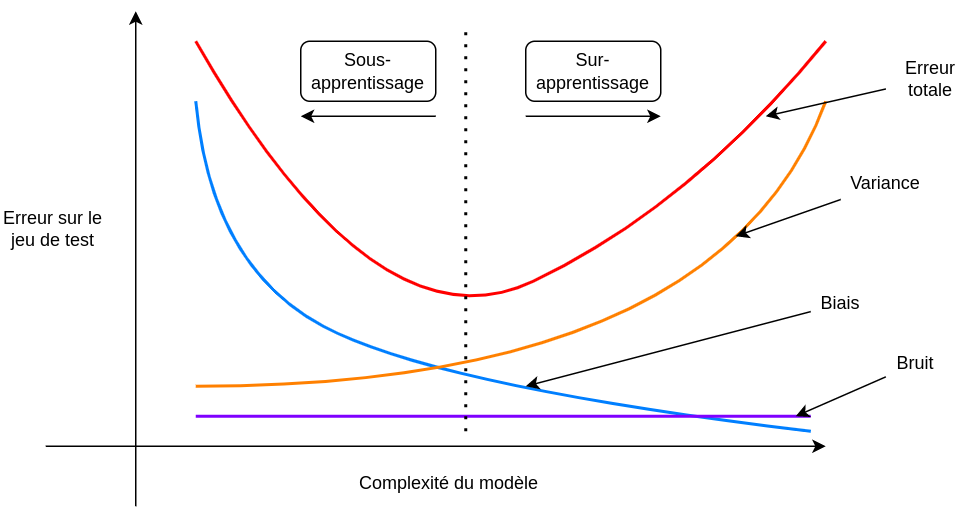
Visualisation¶
On peut imaginer ce que donne un tracé de l’erreur d’un modèle dont on ferait progressivement augmenter la complexité. Petit à petit, l’erreur liée à son biais diminue, mais celle liée à la variance augmente. On peut distinguer alors les deux régimes de sous-apprentissage et de sur-apprentissage.
En pratique, on préfère prendre un modèle faiblement biaisé et ajouter de la régularisation afin de réduire petit à petit le sur-apprentissage.
(**) Détails mathématiques¶
Soit :
\(x, y\) : Des couples de données où \(x\) est un ensemble de features et \(y\) la valeur à déterminer à partir du vecteur \(x\). Ces couples proviennent d’une distribution de probabilité \(P\) quelconque.
\(D\) : Un jeu de données quelconque constitué de couples \((x_i, y_i)\). \(D\) est la réalisation d’un échantillonage de \(P\). On note \(y_i = y(x_i)\).
\(h\) : Un modèle de ML capable d’apprendre à partir d’un jeu de données \(D\). Si \(h\) a été entraîné sur \(D\), on le note \(h_D\), et on note ses prédictions \(h_D(x)\).
On peut alors décomposer le loss moyen d’un modèle \(h\) :
Où :
Explications des valeurs ci-dessus :
\(\bar h(x)\) représente la prédiction moyenne du modèle \(h\) lorsqu’on l’entraîne sur tous les datasets \(D\) probables provenant de la distribution \(P\).
\(\bar y(x)\) représente la valeur moyenne de \(y\) associée à \(x\). En effet, la valeur de \(y\) peut être bruitée ou même ne pas complètement dépendre de \(x\), donc il faut prendre en compte que même si l’on mesure deux fois le même \(x\), il est possible que l’on se retrouve avec des valeurs de \(y\) différentes.
\(\text{loss}_{\text{test}}(h)\) est la performance moyenne du modèle \(h\) entraîné sur l’ensemble de \(D\) probables et évalué sur l’ensemble des couples \((x, y)\) probables, provenant de la distribution \(P\).
La variance est une mesure de l’écart moyen entre la prédiction d’un modèle entraîné avec un dataset \(D\) lambda et la prédiction espérée \(\bar h(x)\) de l’ensemble des datasets.
Le biais est une mesure de l’écart moyen entre la prédiction espérée \(\bar h(x)\) et la valeur espérée \(\bar y(x)\).
Le bruit mesure la variance moyenne entre points \(y(x)\) et leur moyenne \(\bar y(x)\)
Il faut savoir que les modèles \(h\) ne sont pas tous égaux dans cette équation. Une fois que l’on choisit d’utiliser un modèle linéaire, le biais sera forcément très fort. Si le biais n’est pas bon (c.a.d. si \(\bar h(x)\) est loin de \(\bar y(x)\)), notre modèle aura de la peine à faire diminuer le loss. Au contraire, un réseau de neurones peut plus facilement contrôler la force de son biais à travers plusieurs mécanismes de régularisation. Cela nous permet mieux choisir la force des biais et de la variance de notre modèle.
Si ici on utilise \(h\) pour désigner un modèle, c’est parce que l’on considère qu’un modèle est pleinement défini par ses hypothèses.
No Free Lunch (NFL)¶
Le théorème du NFL statue qu’aucun algorithme de recherche de solution n’est meilleur que les autres sur tous les problèmes possibles. La recherche d’un unique algorithme qui serait meilleur que tout les autres est donc inutile. Il est nécessaire de faire des hypothèses sur les biais qui seraient intéressants, afin de choisir le ou les modèles de Machine Learning à entraîner.
Gardez cela en tête, il n’est pas possible de faire un modèle universel !
Le résultat sous-jacent est un peu plus profond que cela, et il existe en fait plusieurs versions de ce théorème. Vous pouvez creuser le sujet de votre côté si vous le souhaitez.
Conclusion¶
Les biais inductifs représentent toutes les hypothèses que l’on fait pour réduire l’espace de recherche des solutions.
Il est nécessaire de choisir les bons biais qui permettront à un modèle de bien généraliser. Ils évitent le sur-apprentissage.
Ces biais doivent être utilisés avec parcimonie afin d’éviter le sous-apprentissage.
La variance d’un modèle caractérise la sensibilité du modèle au jeu d’entraînement. Elle augmente avec la taille de l’espace de recherche.
Avoir beaucoup de données permet l’utilisation de modèles plus expressifs (avec peu de biais et beaucoup de variance), tout en évitant le sur-apprentissage. Les données supplémentaires peuvent être vues comme un moyen de régulariser l’entraînement.
Il n’existe pas de modèle universel meilleur que tous les autres sur n’importe quel jeu de données.