Chapitre II: Notions générales
Contents
Chapitre II: Notions générales¶
Sommaire¶
Modélisation statistique du langage¶
Maintenant que nous avons vu comment préparer le texte avant son utilisation dans un algorithme de NLP, nous nous intéresserons à la représentation des phrases d’un point de vue statistique.
Il est difficile pour un algorithme de travailler avec du texte, mais si nous pouvons convertir ce texte en une suite de chiffres alors nous pourrons en tirer certaines informations qui permettront à l’algorithme de travailler.
Nous étudierons deux techniques de modélisation statistique du texte:
Bag of Words (BoW)
Term Frequency-Inverse Document Frequency (TF-IDF)
Cependant des méthodes plus pointues existent afin d’identifier des corrélations entre des mots avec la modélisation de topics. (groupes de mots ayant une forte probabilité d’être associés)
Nous étudierons en particulier une méthode de modélisation de topics: Latent Dirichlet Allocation (LDA)
Bag of Words (BoW)¶
Bag of Words ou Sac de Mots est une technique de modélisation du texte sous forme de vecteur où chaque élément représente la fréquence d’un token (ici mots) dans le document.
Par exemple:
John aime regarder des films, Mary aime les films aussi.
Deviendra, après tokenisation et regroupement des mots:
"John", "aime", "regarder", "des", "films", "Mary", "les", "aussi"
On obtiendra alors la répresentation vectorielle suivante:
[1, 2, 1, 1, 2, 1, 1, 1]
Ce vecteur ne préserve pas l’ordre des mots.
Implémentation en Python:¶
Il est possible de le programmer soi-même ou d’utiliser une librairie Python telle que scikit-learn qui fera aussi le pré-processing:
from sklearn.feature_extraction.text import CountVectorizer
from nltk.corpus import stopwords
sentence = "John aime regarder des films, Mary aime les films aussi."
CountVec = CountVectorizer(ngram_range=(1,1), stop_words=stopwords.words('french'))
Count_data = CountVec.fit_transform([sentence])
print(CountVec.get_feature_names_out())
print(Count_data.toarray())
On obtient alors:
['aime' 'aussi' 'films' 'john' 'mary' 'regarder']
[[2 1 2 1 1 1]]
Cependant nous pouvons nous poser la question de la pertinence de cette information: un mot fréquent est il porteur de sens ?
La réponse est non, si un mot survient plusieurs fois dans un document mais aussi dans un nombre important de documents alors, peut être, que ce mot est juste un mot fréquent comme une conjonction de coordination, sans sens particulier donc.
Term Frequency-Inverse Document Frenquency (TF-IDF)¶
Afin de remédier au problème du Sac de Mots une approche serait de redéfinir la fréquence des mots afin de constituer un indice qui permette de connaître l’importance d’un mot dans un corpus de textes, ainsi les mots présents dans de nombreux documents seront pénalisés.
Pour cela on utilise deux indices que l’on multipliera:
Term Frequency
Inverse Document Frequency
Tout d’abord le Term Frequency ou la fréquence des termes se calcule de la manière suivante:
Ensuite nous avons l’Inverse Document Frequency ou fréquence inverse du document qui est calculée en prenant le nombre total de documents du dataset, le divisant par le nombre de document contenant le mot puis en appliquant un logarithme:
Enfin nous multiplions ces deux termes pour obtenir le Term frequency-Inverse Document Frequency (TF-IDF):
Implémentation en Python:¶
import re
import nltk
import unidecode
from nltk import word_tokenize
from nltk.corpus import stopwords
from nltk.stem import SnowballStemmer
from sklearn.feature_extraction.text import TfidfVectorizer
def text_processing(text):
''' Return cleaned text for Machine Learning '''
REPLACE_BY_SPACE_RE = re.compile('[/(){}\[\]\|@,;]')
NEW_LINE = re.compile('\n')
BAD_SYMBOLS_RE = re.compile('[^0-9a-z #+_]')
STEMMER = SnowballStemmer('french')
text = text.lower()
text = unidecode.unidecode(text)
text = NEW_LINE.sub(' ',text)
text = REPLACE_BY_SPACE_RE.sub(' ',text)
text = BAD_SYMBOLS_RE.sub(' ',text)
text = ' '.join([STEMMER.stem(word) for word in word_tokenize(text)])
return text
sentence1 = "John aime regarder des films, Mary aime les films aussi."
sentence2 = "Bertrand aime les pizzas, mais les pizzas ne l'aiment pas en retour."
sentence3 = "Le muay thai est supérieur au kick boxing qui est lui même supérieur à la boxe anglaise"
tf_idf_vec = TfidfVectorizer(use_idf=True, ngram_range=(1,1), stop_words=stopwords.words('french'))
tf_idf_data = tf_idf_vec.fit_transform([text_processing(sentence1),text_processing(sentence2), text_processing(sentence3)])
print(tf_idf_vec.get_feature_names_out())
print(tf_idf_data.toarray())
On obtient alors:
['aim' 'aiment' 'anglais' 'auss' 'bertrand' 'box' 'boxing' 'film' 'john'
'kick' 'mary' 'mem' 'muay' 'pizz' 'regard' 'retour' 'superieur' 'thai']
[[0.4736296 0. 0. 0.311383 0. 0.
0. 0.62276601 0.311383 0. 0.311383 0.
0. 0. 0.311383 0. 0. 0. ]
[0.27626457 0.36325471 0. 0. 0.36325471 0.
0. 0. 0. 0. 0. 0.
0. 0.72650942 0. 0.36325471 0. 0. ]
[0. 0. 0.30151134 0. 0. 0.30151134
0.30151134 0. 0. 0.30151134 0. 0.30151134
0.30151134 0. 0. 0. 0.60302269 0.30151134]]
Malheureusement le Stemmer a commis quelques erreurs par exemple ‘aim’ et ‘aiment’ ou ‘box’ et ‘boxing’ qui pourtant devraient avoir la même racine.
Modélisation de topics: Latent Dirichlet Allocation (LDA)¶
Cette partie va vous faire comprendre l’intérêt des mathématiques et des statistiques en particulier pour établir des modèles et des solutions en machine learning.
Latent Dirichlet Allocation ou Allocation de Dirichlet Latente est un algorithme génératif probabiliste permettant la génération de groupes de mots ayant une forte corrélation nommés topics, cet algorithme est particulièrement utile pour l’exploration de données.
Il sert par exemple à:
Connaître l’idée principale derrière un document.
Trouver un document à partir d’un autre document avec un topic similaire
L’idée derrière l’algorithme LDA est de considérer un document comme un ensemble de topics où chaque topic est caractérisé par sa distribution de mots.
On entraîne alors l’algorithme à reproduire le document de départ à partir de paramètres que l’on optimise en fonction de la ressemblance du document généré avec l’original.
Structure de l'algorithme LDA

Où:
\(\alpha = (\alpha_1, \cdots, \alpha_k)\): distribution de Dirichlet de mots pour l’ensemble des topics (vecteur de réels symbolisant les paramètres de la distribution)
\(\beta = (\beta_1, \cdots, \beta_k)\): distribution de Dirichlet de topics pour l’ensemble des documents
\(\theta_m\): distribution multinomiale de topics pour un document m
\(\phi_k\): distribution multinomiale de mots pour un topic k
\(z_{m,n}\): topic pour le n-éme mot dans le document m
\(w_{m,n}\): mot spécifique
La probabilité de générer un document à partir de ce modèle est la suivante:
Pour comprendre cette formule il faut d’abord comprendre comment fonctionnent les distributions de Dirichlet et les distributions multinomiales.
Distribution de Dirichlet:¶
La distribution de Dirichlet ou distribution bêta multivariée est une distribution de probabilités multivariées continues paramétrées par un vecteur de réels positifs \(\alpha = (\alpha_1, \cdots, \alpha_K)\) avec un ordre \(K \ge 2\).
Elle possède une fonction de densité de probabilité qui est la suivante:
Où:
\(x_k\): variable aléatoire
\(\alpha_k\): paramètre à faire varier
\(B(\alpha)\): constante de normalisation, ici la fonction bêta multivariée.
Une fonction de densité de probabilité d’une variable aléatoire continue, est une fonction dont la valeur à tout échantillon donné dans l’espace échantillon peut être interprété comme une probabilité relative que la valeur de la variable aléatoire soit proche de cet échantillon.
En d’autres termes cela spécifie la probabilité que la variable aléatoire tombe dans une plage de valeurs particulière, en opposition à une valeur donnée.
Prenons \(K = 3\):

On observe que:
Lorsque \(\alpha_k = 1.0\) la répartition des valeurs des variables aléatoires est libre.
Lorsque \(\alpha_k \lt 1.0\) la répartition des valeurs des variables aléatoires tend vers les bords du triangle.
Lorsque \(\alpha_k \gt 1.0\) la répartition des valeurs des variables aléatoires tend vers le milieu.
Ainsi on peut voir une distribution de Dirichlet de topics pour l’ensemble des documents de la manière suivante (en faisant varier les paramètres \(\alpha_k\)):

Distribution multinomiale:¶
La distribution multinomiale est une généralisation de la distribution binomiale qui avec des paramètres n (nombre d’expériences indépendantes) et p (probabilité de succès) représente la distribution de probabilités d’une épreuve de Bernoulli (succès ou échec d’une expérience).
Ici il faut imaginer un dé à 6 faces, la distribution multinomiale représente la probablité pour chaque face de succès ou d’échec pour un nombre n de lancer.
La fonction de densité de probabilité est la suivante:
Il est à noter que dans la théorie bayésienne la distribution multinomiale est le conjugué de la distribution de Dirichlet, cela signifie que l’on peut voir la distribution multinomiale comme une distribution de Dirichlet avec des paramétres \(\alpha = (\alpha_1, \cdots, \alpha_K)\) différents, plus facile à calculer.
Ainsi pour \((p_1, \cdots, p_k)\) un vecteur de paramètres d’une distribution multinomiale:
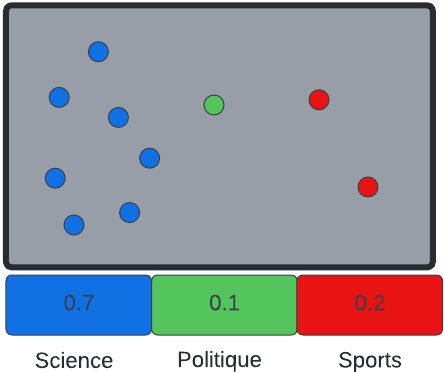
On peut voir une distribution multinomiale de mots par topics de la manière suivante:
Formule complète:¶
Revenons désormais à notre formule décrivant la probabilité de l’algorithme LDA de générer un document spécifique:
On observe que:
\(\prod_{m=1}^{M}{P(\theta_m;\alpha)}\): Distribution multinomiale de topics par documents sachant une distribution de Dirichlet de mots pour l’ensemble des topics.
\(\prod_{k=1}^{K}{P(\phi_k;\beta)}\): Distribution multinomiale de mots par topics sachant une distribution de Dirichlet de topics pour l’ensemble des documents.
\(\prod_{n=1}^{N}P(Z_{m,n} | \theta_m)\): Probabilité d’obtenir un topic pour un mot n donné sachant une distribution multinomiale de topics pour un document m.
\(P(W_{m,n}|\phi Z_{m,n})\): Probabilité d’obtenir un mot sachant une distribution multinomiale de mots pour un topic.
Pour résumer:
On choisit des paramètres \((\alpha_1, \cdots, \alpha_k)\) et \((\beta_1, \cdots, \beta_k)\) pour initialiser une distribution de Dirichlet.
On calcule à partir de ces distributions de Dirichlet des distributions multinomiales.
Ces distributions multinomiales servent à calculer la probablité d’obtenir des topics par mot et réciproquement.
La méthode pour choisir les paramètres \((\alpha_1, \cdots, \alpha_k)\) est d’utiliser le Gibbs sampling ou échantillonage de Gibbs:
Echantillonnage de Gibbs:¶
L’échantillonage de Gibbs est un algorithme utilisant une chaîne de Markov Monte Carlo permettant d’assigner chaque variable aléatoire à un groupe distinct.
Cette forme d’échantillonnage est particulièrement efficace lorsque la distribution des probabilités jointes des variables aléatoires n’est pas connue mais que l’on connaît la distribution conditionnelle de chaque variable.
L’algorithme génére des échantillons conditionnés par la distribution de chaque autre variable, la séquence des échantillons générés ainsi est une chaîne de Markov et la distribution de cette chaîne de Markov est la distribution des probabilités jointes des variables aléatoires.
Chaîne de Markov: une chaîne de Markov est un processus représentant l’évolution d’une variable aléatoire passant d’un état à un autre de manière aléatoire (processus stochastique) indépendamment des états précédents (c’est la condition de Markov)
Méthode de Monte Carlo: méthode algorithmique calculant une valeur numérique en utilisant des procédés aléatoires.
Méthode de Monte Carlo:¶
Supposons que nous souhaitons calculer l’espérance d’une fonction g de la variable aléatoire X tel que \(G = \mathbf{E}(g(X)) = \int g(x)f_X(x)dx\)
La méthode de Monte Carlo consiste à produire un échantillon \((x_1, \cdots, x_N)\) de la variable aléatoire X par rapport à une distribution de probabilités (ici on choisit la distribution uniforme \(f_X(x) = \frac{1}{b-a}\))
Grâce à la loi des grands nombres, qui stipule que l’on peut interpréter la probabilité comme une fréquence de réalisation, on peut utiliser comme estimateur la moyenne empirique \(\bar{g}_N = \frac{1}{N}\sum_{i=1}^{N}g(x_i)\).
Et ainsi \(\mathbf{E}(\bar{g}_N) = G = \mathbf{E}(g(X))\)
Nous avons donc une estimation de l’espérance de G grâce à un échantillon \((x_1, \cdots, x_N)\) de la variable aléatoire X et à un estimateur \(\bar{g}_N\).
Chaîne de Markov Monte Carlo:¶
La différence de cette méthode avec la méthode de Monte Carlo est que pour produire un échantillon \((x_1, \cdots, x_N)\) de la variable aléatoire X nous utilisons une chaîne de Markov et non une distribution de probabilités indépendantes.
En effet les variables aléatoires sont autocorrélées dans notre exemple; la présence de mots dans un topic ou de topics dans un document influe sur la probabilité d’associer un topic à un mot, c’est pourquoi une chaîne de markov est plus appropriée.
Génération de la chaîne de Markov:¶
On initialise le modèle en choissant des valeurs aléatoires (Affecter des mots à des topics et des documents à des topics).
On sélectionne le topic du mot n sachant la distribution des mots par topic, la probabilité de trouver un topic pour un mot est la suivante:
Où:
\(D_{m,k}\): Nombre de fois qu’un document m utilise un topic k.
\(T_{k,W_{m,n}}\): Nombre de fois qu’un topic k utilise un mot donné.
Le reste on l’a déjà vu
Répéter cette étape jusqu’à avoir assigné tous les mots de l’ensemble des documents.
Mettre à jour les paramètres des distributions de Dirichlet \((\alpha_1, \cdots, \alpha_k)\) et \((\beta_1, \cdots, \beta_k)\) avec l’échantillon généré (la chaîne de Markov).
Implémentation de l’algorithme:¶
Maintenant que nous avons vu la laborieuse théorie, nous pouvons passer à la pratique !
Pour fonctionner l’implémentation LDA de scikit-learn a besoin de prendre en entrée une matrice de termes par document, pour cela nous utiliserons l’algorithme TF-IDF étudié plus haut ainsi que de spécifier le nombre de topics à l’avance.
import re
import nltk
import unidecode
from nltk import word_tokenize
from nltk.corpus import stopwords
from nltk.stem import SnowballStemmer
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.decomposition import LatentDirichletAllocation as LDA
def text_processing(text):
''' Return cleaned text for Machine Learning '''
REPLACE_BY_SPACE_RE = re.compile('[/(){}\[\]\|@,;]')
NEW_LINE = re.compile('\n')
BAD_SYMBOLS_RE = re.compile('[^0-9a-z #+_]')
STEMMER = SnowballStemmer('french')
text = text.lower()
text = unidecode.unidecode(text)
text = NEW_LINE.sub(' ',text)
text = REPLACE_BY_SPACE_RE.sub(' ',text)
text = BAD_SYMBOLS_RE.sub(' ',text)
text = ' '.join([STEMMER.stem(word) for word in word_tokenize(text)])
return text
doc1 = "Tout est bien, sortant des mains de l’Auteur des choses : tout dégénère entre les mains de l’homme. Il force une terre à nourrir les productions d’une autre, un arbre à porter les fruits d’un autre : il mêle et confond les climats, les éléments, les saisons : il mutile son chien, son cheval, son esclave : il bouleverse tout, il défigure tout : il aime la difformité, les monstres : il ne veut rien, tel que l’a fait la nature, pas même l’homme ; il le faut dresser pour lui, comme un cheval de manège ; il le faut contourner à sa mode, comme un arbre de son jardin. Sans cela, tout irait plus mal encore, et notre espèce ne veut pas être façonnée à demi. Dans l’état où sont désormais les choses, un homme abandonné dès sa naissance à lui-même parmi les autres serait le plus défiguré de tous. Les préjugés, l’autorité, la nécessité, l’exemple, toutes les institutions sociales, dans lesquelles nous nous trouvons submergés, étoufferaient en lui la nature, et ne mettraient rien à la place. Elle y serait comme un arbrisseau que le hasard fait naître au milieu d’un chemin, et que les passants font bientôt périr, en le heurtant de toutes parts et le pliant dans tous les sens."
doc2 = "Le deuxième volet du sixième rapport d’évaluation du Giec a été publié le 28 février 2022. Le premier volet, en date d'août 2021, concluait que le changement climatique était plus rapide que prévu. Ces derniers travaux s’intéressent aux effets, aux vulnérabilités et aux capacités d’adaptation à la crise climatique."
doc3 = "L’histoire de la vigne et du vin est si ancienne qu’elle se confond avec l'histoire de l’humanité. La vigne et le vin ont représenté un élément important des sociétés, intimement associés à leurs économies et à leurs cultures. Le vin synonyme de fête, d'ivresse, de convivialité, qui a investi le vaste champ des valeurs symboliques, est aujourd'hui présent dans la plupart des pays du monde. Son existence est le fruit d’une longue histoire mouvementée."
tf_idf_vect = TfidfVectorizer(use_idf=True, ngram_range=(1,1), stop_words=stopwords.words('french'))
tf_idf_matrix = tf_idf_vect.fit_transform([doc1, doc2, doc3])
lda_bow = LDA(n_components=15) #n_components = nombre de topics !
lda_bow.fit(tf_idf_matrix)
for idx, topic in enumerate(lda_bow.components_):
print('Top 5 des mots dans le Topic '+ str(idx) + ':')
print([tf_idf_vect.get_feature_names_out()[i] for i in topic.argsort()[-5:]])
print('')
On obtient alors
Top 5 des mots dans le Topic 0:
['sixième', 'concluait', 'publié', 'volet', 'climatique']
Top 5 des mots dans le Topic 1:
['fête', 'vigne', 'leurs', 'histoire', 'vin']
Top 5 des mots dans le Topic 2:
['naissance', 'mêle', 'préjugés', 'être', 'confond']
Top 5 des mots dans le Topic 3:
['naissance', 'mêle', 'préjugés', 'être', 'confond']
Top 5 des mots dans le Topic 4:
['naissance', 'mêle', 'préjugés', 'être', 'confond']
Top 5 des mots dans le Topic 5:
['naissance', 'mêle', 'préjugés', 'être', 'confond']
...
On observe que le nombre de topic était peut être trop élevé.
